Distinguished Guest Professor: Bernd Neubig, AXTAL Consulting
When faced with quartz crystal data sheets or catalogs, you inevitably are confronted with the term “crystal cut.” What is this all about? This article will serve to clarify the significance of crystal cuts in the performance of crystal oscillators.
In the most common applications quartz crystals are used as a core element to generate a stable frequency. Besides the stability over time (so-called aging), the frequency stability vs. temperature is a primary factor. Therefore, from the early beginning, researchers have looked on the parameters which determine frequency stability over temperature.
Quartz crystals are mechanical resonators that can be electrically forced to vibrate at its mechanical resonance by means of the (inverse) piezo-electric effect. As with every elastic body, in quartz, various “bulk acoustic” resonance modes do exist, such as length or width extensions, flexural modes, shear modes along face or thickness, etc. The resonance is primarily dependent on the frequency-determining dimension, such as length, width, thickness or combinations thereof. The highest frequencies are achieved by the smallest mechanical dimension, i.e., the thickness of the vibrating plate. Such resonances are in the MHz range, while all other resonance modes are in the kHz range
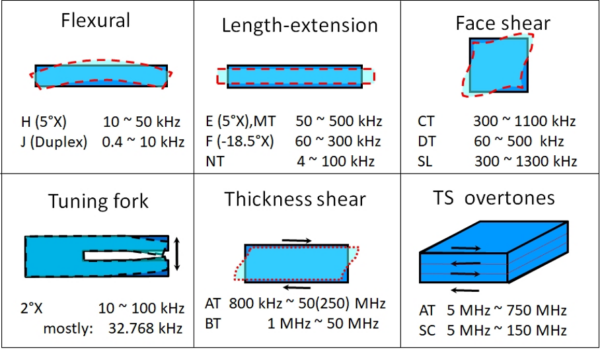
Figure 1. Crystal oscillator vibration modes
Figure 1 depicts several vibration modes that can be used in crystal oscillators. Nowadays, 99.9% of all quartz resonators operating in the kHz or MHz frequency ranges are based on the vibration modes of the second row. Resonators working on the modes depicting in the first row are of historical interest only. Frequencies in the GHz range can be generated by exciting “Surface Acoustic Waves” by means of ultra-fine comb electrode structures on the surface of the crystal plate. Those will not be covered in this article.
Determining the Ideal Cut
Let us take a closer look to the parameters that are governing the resonance frequency. Besides the relevant mechanical dimension t, the resonance frequency is determined by the density and the elastic stiffness of the crystal material. Thus, the frequency / temperature stability is determined by the coefficients of these parameters over temperature.
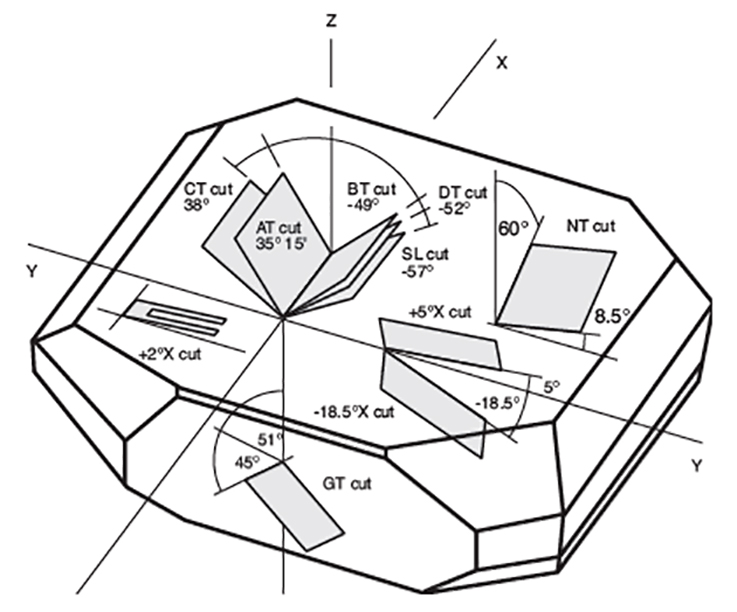
Quartz is an anisotropic material, meaning that the elastic stiffness and its temperature coefficients are different in the different crystal directions (axes). In the first half of the last century this was thoroughly studied for so-called single-rotated crystal cuts. Varying the cut angle Θ (theta) from the Y-axis (Y-cut), several angles possessing zero frequency-temperature coefficients could be identified, as shown below (Figure 2). These cuts were named alphabetically AT, BT, CT, DT ET and FT, where the “T” stands for “Temperature Compensated.”
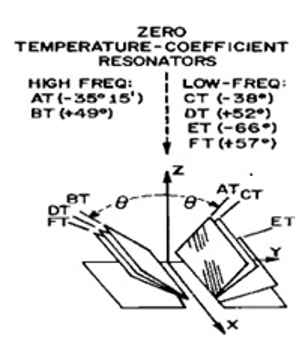
Figure 2. Varying the angle of the cut from the Y-axis yields a number zero
temperature coefficient resonators.
The AT and BT cuts are for the thickness-shear mode (MHz resonators), while the other cuts are for the low-frequency resonators in the kHz range. From these cuts only the AT-cut “survived” until today as an industrial product.
In fact, the ideal AT-cut possesses a zero frequency-temperature coefficient at room temperature, see the green curve in Figure 3 below, which is marked as 0’ (zero angle). However, below and above room temperature the frequency changes in the shape of a 3rd order parabola. If the cut angle is only changed by a few minutes of an arc, the temperature curve is tilted, as can be seen in the chart below.
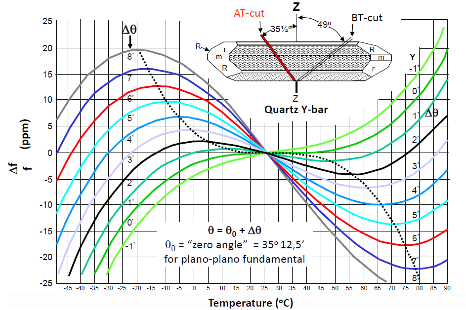
Figure 3. Frequency stability over temperature for an AT-cut crystal resonator
Controlling Temperature to Attain Maximum Frequency Stability
In practice, the optimum cut angle, which allows the smallest possible frequency deviation over a given temperature range, is in the range of 2’ to 4’ (arc minutes from the zero angle). Highest frequency stability can be achieved, if the crystal is operated at a constant temperature in a temperature-stabilized oven. For such applications (oven-controlled crystal oscillators, OCXO) the optimum cut angle is in the range of 6’ to 8’, where the frequency shows a zero slope at the oven temperature (+75°C to 85°C).
In the search for higher stability and less sensitivity to other environmental parameters, double-rotated cuts were evaluated by rotating the AT-cut away from the X-axis by an angle Ø (Figure 4)
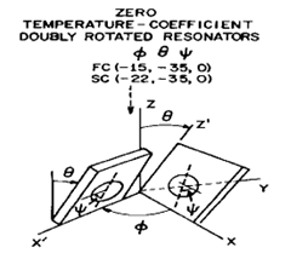
Figure 4. Double rotated cut resonators achieve higher stability
Along this path, several cuts with interesting characteristics could be identified, such as the FC-, the IT- and the SC-cut (Figure 5). Out of these, the SC-cut has become the most popular cut for high-precision, low-noise crystal oscillators. Its zero-temperature coefficient is at about +90°C, making it very suitable for oven-controlled operation. SC-cut crystals are outperforming the AT-cut crystals in OCXO applications due to their higher Q, lower aging, lower phase noise, and lower sensitivity of phase noise to vibrations. SC-cut resonators are nowadays the dominating crystals in high-stability, high performance OCXOs – despite of the higher production cost due to the needed control of two cut angles within tight tolerances.
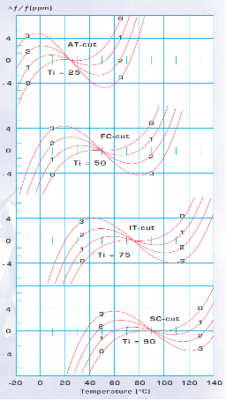
Figure 5. The zero temperature coefficient points for AT, FC, IT and SC-cut crystals
Conclusion
A crystal resonator is capable of achieving a high degree of frequency stability at specific temperatures when the crystal is precisely cut. Today, crystals most commonly utilize the -AT cut. The double-rotated -SC cut further adds to the stability of OCXO oscillators by providing the optimum zero-temperature stability point of 90°.